OKX Research：算法与人性的较量—解析算法稳定币

加密货币领域最让人赞叹的地方在于其不断的创新，而新年伊始开始兴起的算法稳定币，无疑是目前最具野心、最具天马行空想象力的货币创新实验—试图抛弃传统的人为操控，力求以算法本身，实现货币的稳定性。

可以说，开发算法稳定币的尝试是一场算法与人性的较量。算法，追求的是绝对理性，以代码形式呈现事先设定的规则，其运行逻辑不受环境左右；人性，往往在“动物精神”下表现出贪婪和恐惧，引发市场的暴涨暴跌。

然而，这造成了当前算法稳定币普遍存在的一个悖论：在初期，为了实现市场规模的扩张，算法稳定币必须利用人性的贪欲来增发稳定币，但这却是以价格不稳定为代价；当稳定币市场规模足够大后，币值的稳定得到了提高，人们却因无利可图而纷纷离场，造成了市场规模的收缩。

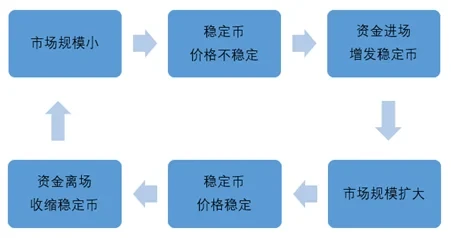
从去年夏天第一代算法稳定币AMPL开始，到如今风头正盛的第二代算法稳定币Basis Cash和ESD，我们都可以观察到算法稳定币在“市场规模-价格稳定”悖论中反复挣扎与撕裂。

1. 第一代算法稳定币— 单币种系统（AMPL）

尽管早在2018年市场上即开始出现算法稳定币，但直到2020年夏天AMPL的出现，算法稳定币才真正引起众人的关注。

从算法原理上看，AMPL并没有特殊之处，其理论基础是经济学中最简单也是最重要的供需模型：AMPL没有总量上限；当AMPL的价格上升，高于1.06美元时，将增加AMPL流通量来降低市场价格；当AMPL的价格降低，低于0.96美元时，将减少AMPL流通量来提高市场价格，以此将AMPL的价格将维持在1美元附近。

有一个笑话说，如果教会鹦鹉说“供给”和“需求”两个词，鹦鹉也能变成经济学家。这虽是调侃，但也说明了供需分析在经济学中的重要地位。很多人在分析AMPL时，喜欢用供需分析中的两句话来说明：

• “稳定币价格上升，导致稳定币供给上升”
• “稳定币供给上升，导致稳定币价格下降”

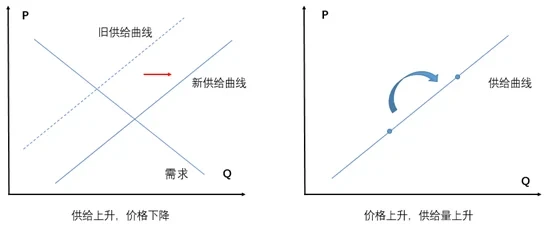
第一句话，看起来没什么问题，因为在现实中也是如此，当商品的价格上涨时，会提高商家的积极性，产出更多的商品；第二句话，也没什么问题，在市场上的商品供给过多时，会导致价格下降。因此很多人喜欢这样解释AMPL的工作原理：

AMPL价格上升 → AMPL供给上升 → AMPL价格下降

如此一来，AMPL便实现了价格的稳定，然而从现实运行情况看AMPL却波动剧烈。原因在于，上述推理看起来做到了逻辑自洽，实际上漏洞百出。其中的关键在于，第一句中的“供给”和第二句中的“供给”是两个不同的概念。

第一句中的“价格上升，供给上升”，这里的“供给”是指“供给量”，即在给定其他条件不变的情况下，价格越高，生产者提供的商品数量越多，从供需图上看，供给量是一个点；第二句中的“供给上升，价格上升”，这里的“供给”应该是指在任何一个给定的价格上，生产者都愿意提供更多的商品，从供需图上看，供给是一条曲线，供给的增加意味着曲线的右移。因此上述两句话完整的陈述应当是：

• 稳定币价格上升 → 稳定币供给量上升（曲线上的点向上移动）
• 稳定币供给上升（曲线向右移动）→ 稳定币价格下降

在区分了“供给”和“供给量”后，我们可以发现，第一代算法稳定币所谓的“供给弹性”，只不过是一种误解—AMPL仍然是一种供给完全无弹性的货币（一条竖直的曲线，造成价格波动更大），只不过依赖了价格这个参数，对供给进行了调节，其现实的运行逻辑是：

• AMPL需求上升（曲线右移） → 价格上升 → AMPL供给上升（算法操纵下，曲线右移）→ AMPL价格下降
• AMPL需求下降（曲线左移） → 价格下降 → AMPL供给下降（算法操纵下，曲线右移）→ AMPL价格上升

对于投机者而言，这是一种利用算法操纵市场的绝妙机会：早期稳定币的流通量较低，容易通过注入资金来低成本地拉高价格（需求曲线右移，推动价格上升），造成稳定币的增发，这些增发的稳定币会分配到持币人手中， 当价格高到一定程度时，持币人再抛售增发的稳定币，以此获取巨额收益。

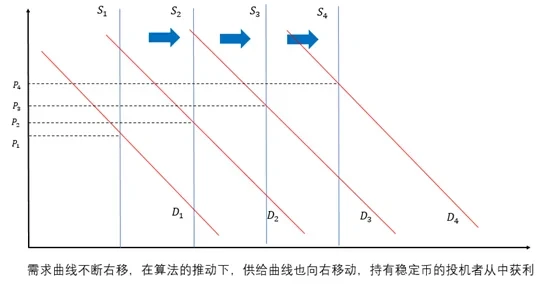
然而，当AMPL的市场流通量大到一定程度时，投机资金想要拉升价格需要付出更多的成本。为此，投机资金开始抛售手中的稳定币并撤出该项目，造成需求的下降（需求曲线的左移），这样的后果是AMPL的价格开始下跌。价格下跌时，在算法的推动下，供给曲线开始右移，这进一步造成了价格的下跌，并推动更多的资金离场，由此形成了“死亡螺旋”，直到市场需求下跌到稳定为止。

从下图AMPL的价格与供应量变化情况也可看出上述现象：在6月时投机资金涌入，不断拉高AMPL的价格，使得AMPL一直增发；到7月时，AMPL的价格已经被拉高到近4美元，继续拉盘的成本过高，投机资金开始退出，投机者抛售手中的AMPL，导致AMPL价格砸穿1美元，随后AMPL供应量开始迅速回落。

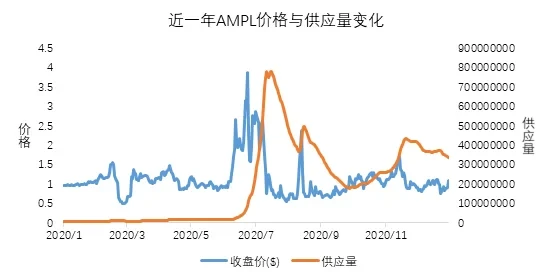
AMPL作为算法稳定币的鼻祖，由于其自身的设计缺陷，造成了投机的盛行和稳定币价格的极度不稳定。从这点看，APML并不算一个成功的算法稳定币项目，在算法与人性的博弈中，算法彻底沦为人性的奴隶，变成投机客收割市场的工具，但其开创意义，仍值得肯定。

2. 第二代算法稳定币— 多币种系统（Basis Cash）

相较于第一代算法稳定币只有一个币种，为了增加系统的稳定性，以Basis Cash和ESD为代表的第二代算法稳定币都增加了系统中的丰富度。

以Basis Cash为例，算法中主要有三个角色：稳定币BAC （Basis Cash）、BAB （Basis Bond）、BAS （Basis Share），根据官方宣传的说法，这三款代币分别对应美元，债券，股票。其稳定机制如下：

• 当BAC价格低于1美元时，用户可以用BAC低价申购债券 BAB（BAB 价格 = BAC 价格的平方），以此减少BAC的流通量，并提高BAC的价格
• 
  当BAC价格高于1美元时，用户可用BAB换取BAC；如果回购BAB结束后仍需要增发BAC，则增发的部分会作为分红分配给BAS的持有者；通过上述方式增加BAC的流通量，以降低BAC价格。

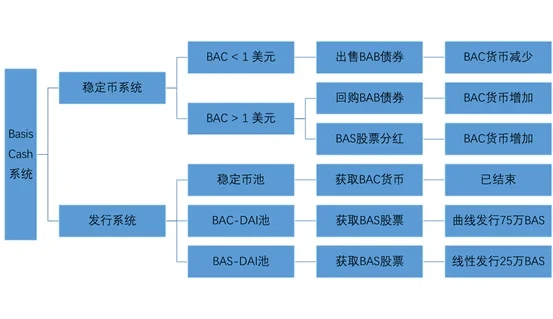
在币种的发行方面，Basis Cash的主要设计了三个流动性池：

首先是稳定币池，在项目初期，用户可通过存入DAI （MCD）、yCRV、USDT、sUSD 和 USDC到相关的合约池里，获取新的BAC作为收益，目前该池已经关闭；

其次是Basis Share 1 池，用户需要向 Uniswap V2 的 DAI-BAC池提供流动性，获取LP代币后存入1池即可享受BAS收益。根据设计，1池将会分配总计 750,000 枚BAS；

最后是Basis Share 2 池，用户将向 Uniswap V2 的 DAI-BAS池提供流动性，获取LP代币后存入2池即可享受BAS收益。根据设计，1池将会分配总计 250,000 枚BAS；

从上可以看出，Basis Cash的稳定币设计机制，模拟的是中央银行的公开市场操作（Open market operations）：当市场资金过剩时，央行卖出债券，从市场回笼货币；当市场资金紧缺时，央行买入债券，向市场投放货币。这也是Basis Cash官方一直所宣扬的—打造“去中心化的美联储”。

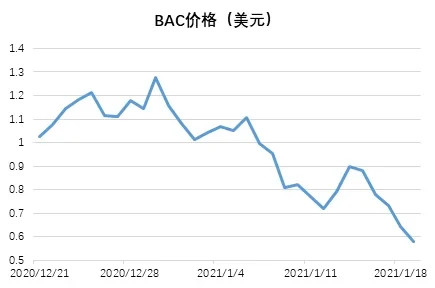
然而，从实际情况上看，BAC在上市后价格剧烈波动，并未表现出稳定的特性，目前BAC的价格已经跌破0.6美元的关口—即出现了40%的负溢价，但价格依然没有出现回升的趋势。为什么号称“去中心化美联储”的Basis Cash最终也没实现对价格的稳定控制呢？因为Basis Cash只学到了现代中央银行的表象和皮毛，而没学到精髓。这具体表现在Basis Bond的定性和货币政策工具的设计上。

（1）Basis Bond究竟是什么？

按照官方的说法，Basis Cash发行的Basis Bond（BAB）是一种债券。实际上，BAB并不是一种债券（Bond），而是一种永续的上涨-敲入看涨期权（up-and-in-call）。

理解这一点很关键，债券是面向债权人发行，并承诺在特定的日期还本付息，这无关乎标的物价格的高低—即使在未来BAC价格一直低于1美元，也不影响债权的偿还支付。因此，央行在市场上发行央行票据时，有投资者愿意购买，并成功回笼市场上的资金。

那什么Basis Bond（BAB）是上涨- 敲入看涨期权呢？因为只有当标的资产BAC的价格上涨到1美元时，系统才允许投资者行使买入BAC的权利，其中的收益=当前的BAC价格 – 买入BAB时BAC价格的平方。例如一个投资者在BAC为0.9美元时，以0.81美元的代价买入一个BAB；当BAC价格上涨至1.5美元时，触发期权生效条件，若此时投资者行权并获得一个BAC，那么其收益为 1.5 – 0.81 = 0.69美元；而如果BAC的价格一直低于1美元，那么将无法出发Basis Bond的行权条件，此时对于投资者而言Basis Bond就是一张“废纸”。

可以说，Basis Bond的奇异期权本质，导致了Basis Bash“公开市场操作”的失灵，投资者购买Basis Bond，其信心并不是基于Bond本身在到期时的还本付息，而是押注BAC价格将来会回到1美元上方，赌的是市场对BAC的信心，赌的是BAC的未来。

这就好比在BTC价格下跌时，一些带单分析师告诉投资者一定要趁现在加杠杆大量买入BTC，其逻辑是：只要大家购入BTC，就会减少BTC的流通量，进而抬高BTC的价格，随后可以获取一笔不菲的收益。有多少投资者愿意买单呢？相信市场已经给出了答案。

（2）Basis Cash是不是合格的“去中心化美联储”？

真正的公开市场操作，要求央行既有可以释放流动性的工具，也有收回流动性的工具。从公开市场操作的品种种类看，目前公开市场操作业务主要包括回购交易；现券交易和中央银行票据，具体业务如下所示：

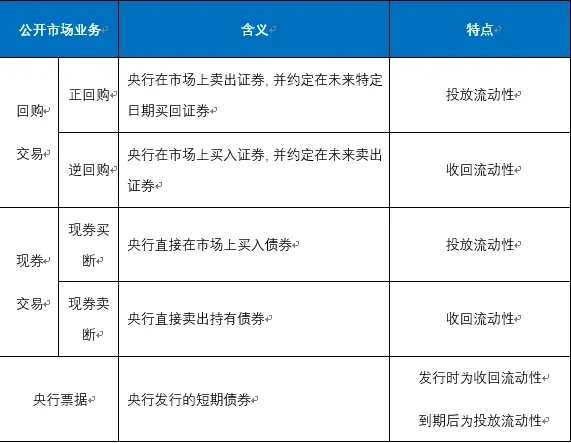
虽然Basis Cash号称“去中心化的中央银行”，但其模仿的仅仅是央行票据这一工具，只能通过发行Basis Bond（BAB）来收回流动性，但在面临市场流动性紧缺（BAC > 1 美元）时，却没有足够的工具来为市场注入流动性。因此这又不得不回到了AMPL的老路：通过直接控制稳定币的供应量来注入流动性。

虽然Basis Cash存在种种不足，但相较于AMPL仍然是一大进步，尤其是在抑制稳定币的增发冲动方面。对于AMPL而言，由于采用单币种系统，AMPL持币者本身可以获取稳定币增发的分红，造成了投机的盛行；而采用多币种的Basis Cash，在稳定币增发时首先回购Basis Cash，随后才分发给Basis Share持有人；另一方面， Basis Cash还在不断地增发，两方面因素共同作用，抑制了投机性资金对Basis Cash过度冲击。

3. 第三代算法稳定币—半抵押型（FRAX）

在目前的市场上，半抵押型算法稳定币的代表是FRAX，与第一代和第二代算法稳定币所不同的是，FRAX的铸造和销毁都是以两种财富为基础—传统稳定币USDC和系统财务“FXS”，即

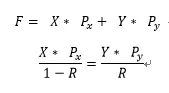
其中，F 为新铸造的FRAX的数量，X为FXS的数量， 为FXS的美元价格,Y为传统稳定币USDC的数量， 为USDC的美元价格，R为抵押率

抵押率R根据系统算法进行调整：开始运行时，FRAX的抵押率为100% ，每个小时调整一次（根据区块数确定），最开始的 1 小时内，铸造一个 FRAX就需要 1 美金的传统稳定币作为抵押品。从此每隔一小时后：

• 如果PUSD > 1 USD ，在本次调整中，抵押率将下调 0.25%。
• 如果PUSD < 1 USD ，在本次调整中，抵押率将上调 0.25%。

为了保证实际抵押率等于算法设定的抵押率，FRAX还设计了“回购（Buybacks）和再抵押（Recollateralization）机制”。首先是再抵押机制，当算法将系统抵押率上调时，为了使实际抵押率等于系统抵押率，必须增加系统中的USDC数量，FRAX设置了一个激励措施：任何人都可以向系统中添加USDC，并换取更多数量的FXS；例如一个用户可以向系统中添加价值1美元的 USDC，换取价值1.2美元的FSX。“回购机制”则是当系统抵押率下调时，用户可随时用FXS向系统换取同等价值的USDC，因此在回购机制中不存在奖励措施。

“回购（Buybacks）和再抵押（Recollateralization）机制”的存在，保证了用户可以随时按照算法给定的抵押率，铸造或赎回稳定币FRAX，防止出现了USDC抵押品不足的现象。此时，在套利机制的作用下，保证了FRAX价格的稳定性：

• 当 1 FRAX < $ 1时，套利者会购买 FRAX，并以 FRAX 去赎回 USDC 和 FXS，并通过出售 FXS 获利。对 FRAX 的购买需求将让FRAX价格上涨。
• 当 1 FRAX > $ 1，套利者将通过 USDAC 和 FXS 去铸造 FRAX，并卖出 FRAX 而获利，卖出压力将促使FRAX价格下跌。

从上可以看出，尽管FRAX声称是“半抵押型”算法稳定币，实际上它是一种“全抵押型”算法稳定币—用户可以随时用1 FRAX换取价值1 美元的USDC和FRX，算法控制的只不过是系统的抵押率和FXS的增发速率，所以FRAX的价格异常稳定。

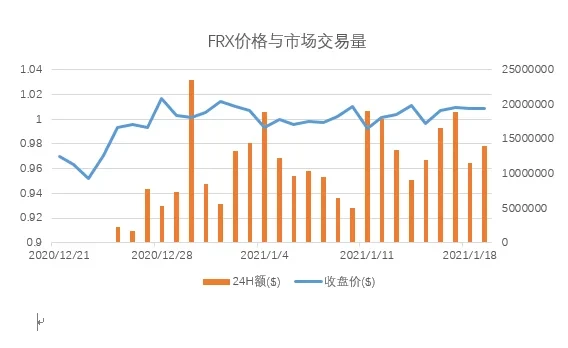
当然，FRAX的问题在于：FXS从实际情况上看完全没有任何价值，套利者在任何时刻都可以用1 FRAX换取 价值1 美元的USDC和FXS，这意味着系统将稳定币的价格波动风险完全转移给了FXS的持有者。毕竟价值1美元的FXS，可以是“价格为0.01美元的100 FXS”，也可以是“价格为 0.001 美元的1000 FXS”。

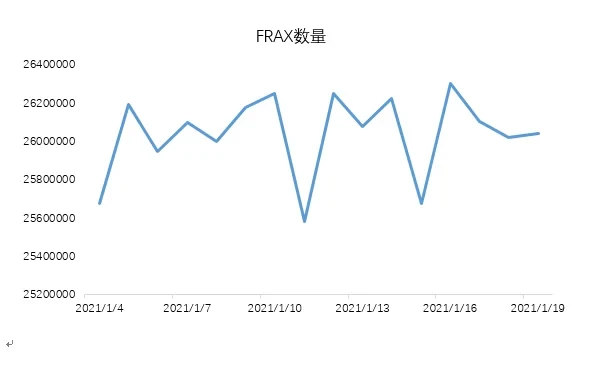
更重要的是，第一代和第二代算法稳定币的市场规模扩张依赖于投机，而FRAX却去除了投机攻击的可能—这意味着FRAX市场规模增长的缓慢。如下图所示，今年发行以来，FRAX的发行量迟迟未突破2,600万。为此，FRAX在未来需要建立属于自己的“债务市场”或其他能创造财富的市场，才能实现FRAX规模的迅速扩张。

4. 算法稳定币的未来

在现代经济条件下，货币投放主要存在两大渠道：

一是货币投放机构通过购买货币储备物或价值锚定物（如黄金、外汇等的价值储藏品）相应投放货币，据以确定货币的单位价值，并增强货币的可信度。

二是由货币投放机构通过向社会主体发放贷款或购买其债券等方式投放的货币。贷款和债券，都代表着未来的财富，这就脱离了当前现实财富的限制，据以投放货币，将能够保证货币的及时供应，以及货币总量与财富规模的基本对应，以此保证金币值的稳定。

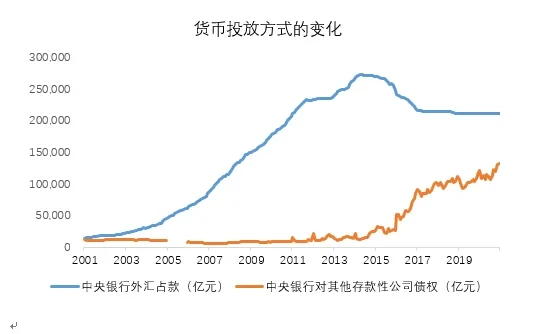
以中国为例，在2000-2014年之间，人民币的发行主要以外汇占款为主，原因在于在这段时期中国的对外出口迅速增加，央行为了稳定币人民币汇率，不得不收购大量的美元等外汇资产，进而投放出大量的人民币，即人民币的增发是建立在美元等外汇资产的基础上；自2014年后，中国的外汇占款开始逐年下滑，此时人民币的发行又演化成以国内银行体系的负债增加为主导，即人民币的发行建立在债务的基础上。

    同样地，第一代稳定币，如USDT、USDC等都是如此：每发行1稳定币背后，都有1美元的现实法币作为储备（尽管部分非合规稳定币存在猫腻），以此维持稳定币的信心，保证了稳定币价格的稳定。

而当前各类算法稳定币存在“市场规模-价格稳定”悖论的根本原因在于：算法稳定币的投放不是按当下或未来财富规模的大小进行投放，容易引发投机，并以此实现稳定币规模的扩张，其后果是币值的极度不稳定和项目的不可持续性。

同样地，目前市场上存在一种谬误：算法稳定币市场规模的扩张，必须依托于投机，因此可以牺牲算法稳定币价格的不稳定。这本身就是对市场经济认识的不深刻，货币规模的扩张，取决于社会财富的增长。投机带来的财富是暂时性的，因为它没有创造财富，只是利用市场规则转移了财富，所以当投机资金撤离时，项目也会衰亡。

当前的算法稳定币普遍缺乏一个可以创造财富的市场。因此，如果算法稳定币想在未来取得成功，必须为算法稳定币建立一个“债务市场”或“财富创造市场”，这一市场在DeFi领域可以是借贷协议、保险协议或其他有实际应用价值的协议。以当前和未来的财富规模作为基础，进行算法稳定币的投放与回笼。这既能解决“市场规模-价格稳定”悖论，又能为算法稳定币创造足够的“政策工具”来维持价格的稳定。