Zero-Knowledge Proofs : que sont les zk-STARK et comment fonctionnent-ils ? (zk-Stark V2)

Qu’est-ce que la preuve de réserves et la preuve à divulgation nulle de connaissance ?

Preuve de réserves (PoR)

La preuve de réserves ou Proof-of-Reserve (PoR) est un processus qui permet aux plateformes d’échange de cryptomonnaies de montrer qu’elles ont suffisamment d’actifs pour couvrir tous les soldes des clients. Cela renforce la confiance en prouvant que la plateforme d’échange ne cache pas de dettes. La manière la plus simple d’en apporter la preuve est de publier à la fois les montants d’actifs de la plateforme d’échange et une liste des soldes des utilisateurs afin que tout le monde puisse confirmer :

• La valeur totale des actifs que OKX prétend détenir correspond à la somme du solde total des actifs de chaque utilisateur

• Le solde total de chaque utilisateur est supérieur à zéro, et leurs actifs sont pris en compte, couvrant leurs passifs et garantissant que chaque utilisateur a un capital net positif

• La valeur totale indiquée par la plateforme d’échange tient compte de chaque utilisateur, chacun devant donc être en mesure de vérifier que sa valeur nette est incluse dans la valeur totale

Cependant, révéler ces soldes peut compromettre la confidentialité des utilisateurs. Pour résoudre ce problème, nous utilisons une méthode appelée preuve à divulgation nulle de connaissance ou Zero Knowledge Proof (ZKP) pour protéger la vie privée de l’utilisateur.

Preuve à divulgation nulle de connaissance (ZKP)

Cette technique de sécurité permet à la plateforme d’échange de cryptomonnaies de prouver qu’une déclaration est vraie sans révéler d’informations supplémentaires.

Dans notre cas, nous voulons prouver que nous avons suffisamment de fonds sans partager les détails spécifiques des utilisateurs. La plupart des ZKP relèvent de deux catégories :

• zk-SNARK

• zk-STARK

Nous utilisons zk-STARK, car il est plus sécurisé et a une hypothèse de sécurité minimale. Dans cet article, nous vous expliquons comment nous utilisons zk-STARK pour protéger la confidentialité des utilisateurs tout en prouvant notre solvabilité.Avant de continuer, il est utile de connaître certains termes ZKP de base, comme « circuit », « arbre de Merkle » et « engagements ».

Pour les débutants, il existe de nombreuses ressources disponibles pour vous aider à vous lancer. Pour les utilisateurs avancés, vous pouvez vous référer au cours MOOC et à la monographie académique.

Comment fonctionne zk-STARK ?

Nous créons un arbre de Merkle en utilisant le hachage du compte de chaque utilisateur comme feuilles. Chaque compte affiche des soldes en USD pour divers jetons (parexemple, BTC, ETH). Pour gérer ces soldes, nous séparons ses soldes en fonds propres non négatifs et en dettes pour chaque jeton. De cette façon, nous ne travaillons qu’avec des nombres positifs, ce qui facilite le traitement des calculs et évite les erreurs.

Par exemple :

• Si le solde de jetons BTC d’un utilisateur est A, ses fonds propres en BTC correspondent à A et sa dette en BTC à 0.

• Si le solde de jetons ETH d’un utilisateur est -B, ses fonds propres correspondent à 0 et sa dette à B.

Ensuite, nous construisons un arbre de Merkle avec ces valeurs de compte comme feuilles. La racine de l’arbre fait office de valeur unique représentant tous les soldes des utilisateurs. Chaque utilisateur peut prouver que son compte fait partie de cet arbre en utilisant un chemin de Merkle, qui montre comment son compte se connecte à la racine.

Nous publions également les fonds propres totaux et les dettes cumulées de tous les jetons et utilisateurs. Ensuite, nous créons une preuve à divulgation nulle de connaissance (ZKP) pour montrer deux choses :

• Preuve de somme : les valeurs des fonds propres et des dettes dans l’arbre de Merkle s’additionnent correctement

• Preuve non négative : les fonds propres totaux de chaque utilisateur sont supérieurs à la dette totale

Lorsque nous essayons de vérifier l’arbre de Merkle pour un grand nombre de comptes, cela devient trop difficile à gérer en une seule fois. Pour surmonter ce défi, nous divisons les comptes en plus petits groupes appelés lots. Chaque lot est traité séparément en utilisant des circuits de lot ou « batch circuits », qui vérifient la partie inférieure de l’arbre de Merkle.

Le traitement par lots le rend non seulement gérable, mais nous permet également d’exécuter ces vérifications en même temps (traitement parallèle). Une fois que nous avons les résultats de chaque lot, nous utilisons une autre couche de circuits, appelée circuits récursifs, pour combiner et vérifier tous les lots ensemble, jusqu’à ce que nous ayons prouvé l’ensemble de l’arbre de Merkle.

Qu’est-ce qu’un circuit de lots ?

Le circuit de lots prend en charge 1 024 comptes (acc₀, acc₁,..., acc₁₀₂₃) en tant qu’entrées et génère 3 sorties principales : un hachage (h_batch), une valeur totale pour les fonds propres (e_batch), et une valeur totale pour la dette (d_batch). Il vérifie que :

• La valeur totale des fonds propres libellés en USD de chaque compte est supérieure à son total de dettes

• e_batch est la somme de toutes les valeurs pour les fonds propres libellés en USD dans ces comptes

• d_batch est la somme de toutes les valeurs pour les dettes libellées en USD dans ces comptes

• h_batch est la racine de l’arbre de Merkle créée en utilisant les hachages des comptes

• Il n’y a pas de débordement au moment de faire la somme pour e_batch et d_batch

Qu’est-ce qu’un circuit récursif ?

Le circuit récursif intègre 64 preuves différentes (π₀, ..., π₆₃), les hachages (h₀, ..., h₆₃), les fonds propres (e₀, ..., e₆₃₎, et les dettes (d₀, ..., d₆₃) des circuits de couche inférieure en tant qu’entrées. Il combine ces entrées et produit 3 sorties : un nouveau hachage (h_recursive), les fonds propres totaux (e_recursive), et la dette totale (d_recursive). Il vérifie que :

• Chacune des 64 preuves est valide

• Chaque preuve π₀, ..., π₆₃ du circuit de couche inférieure est valide

• e_recursive est la somme de e₀, ..., e₆₃

• d_recursive est la somme de d₀, ..., d₆₃

• h_recursive est le hachage de la concaténation de h₀, ..., h₆₃, i.e.

  • h_recursive = Hash (h₀ || h₁ || ... || h₆₃₎

• Il n’y a pas de débordement au moment de faire la somme pour e_recursive et d_recursive

Quelle est le rapport entre les circuits de lots et les circuits récursifs ?

Le diagramme ci-dessous illustre comment le circuit de lots et les circuits récursifs se connectent et échangent des données entre eux. Gardez à l’esprit que dans ce diagramme, nous dupliquons les circuits à des fins d’illustration, mais que dans les faits, nous n’utilisons qu’un seul circuit pour chaque couche.

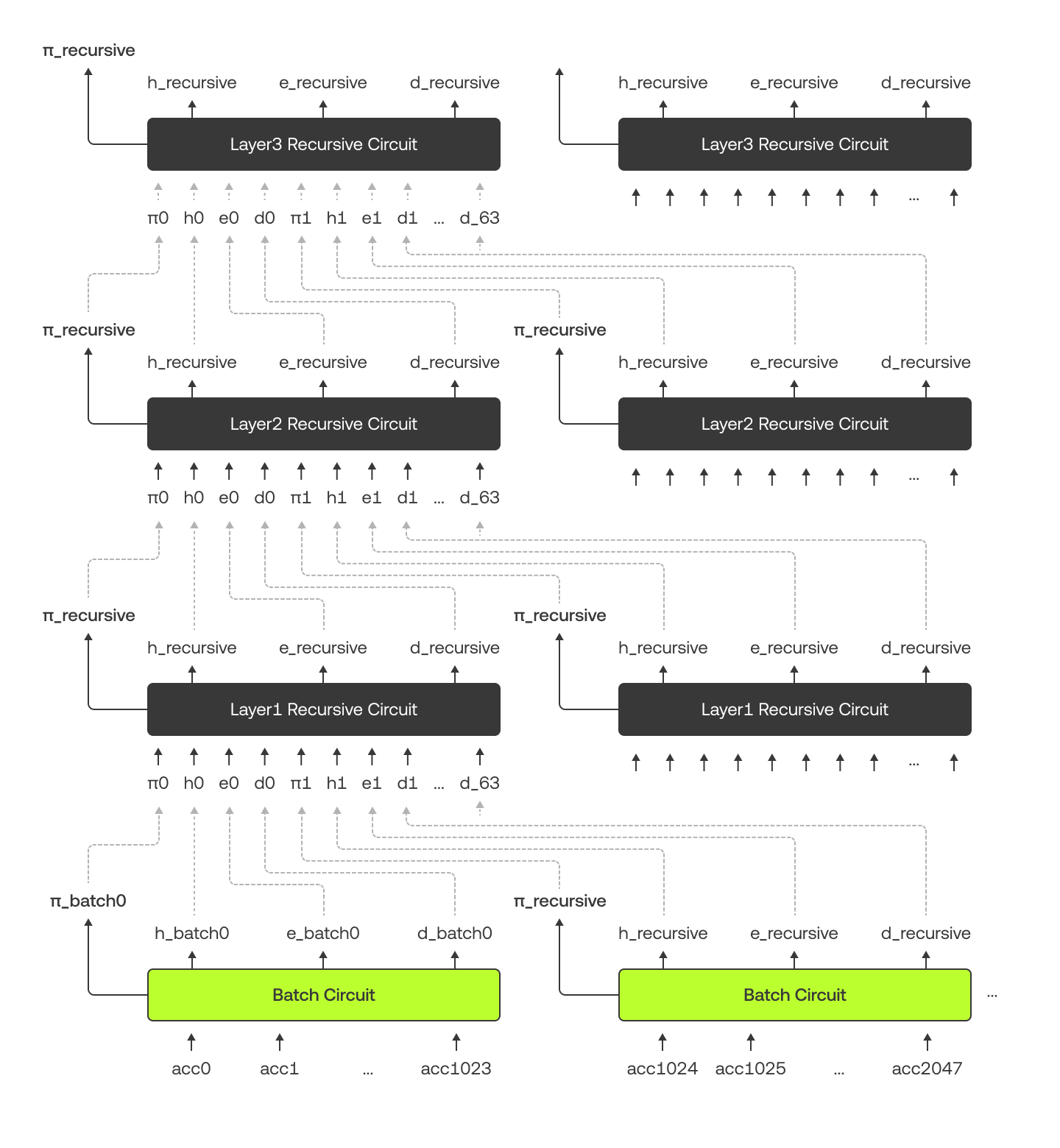
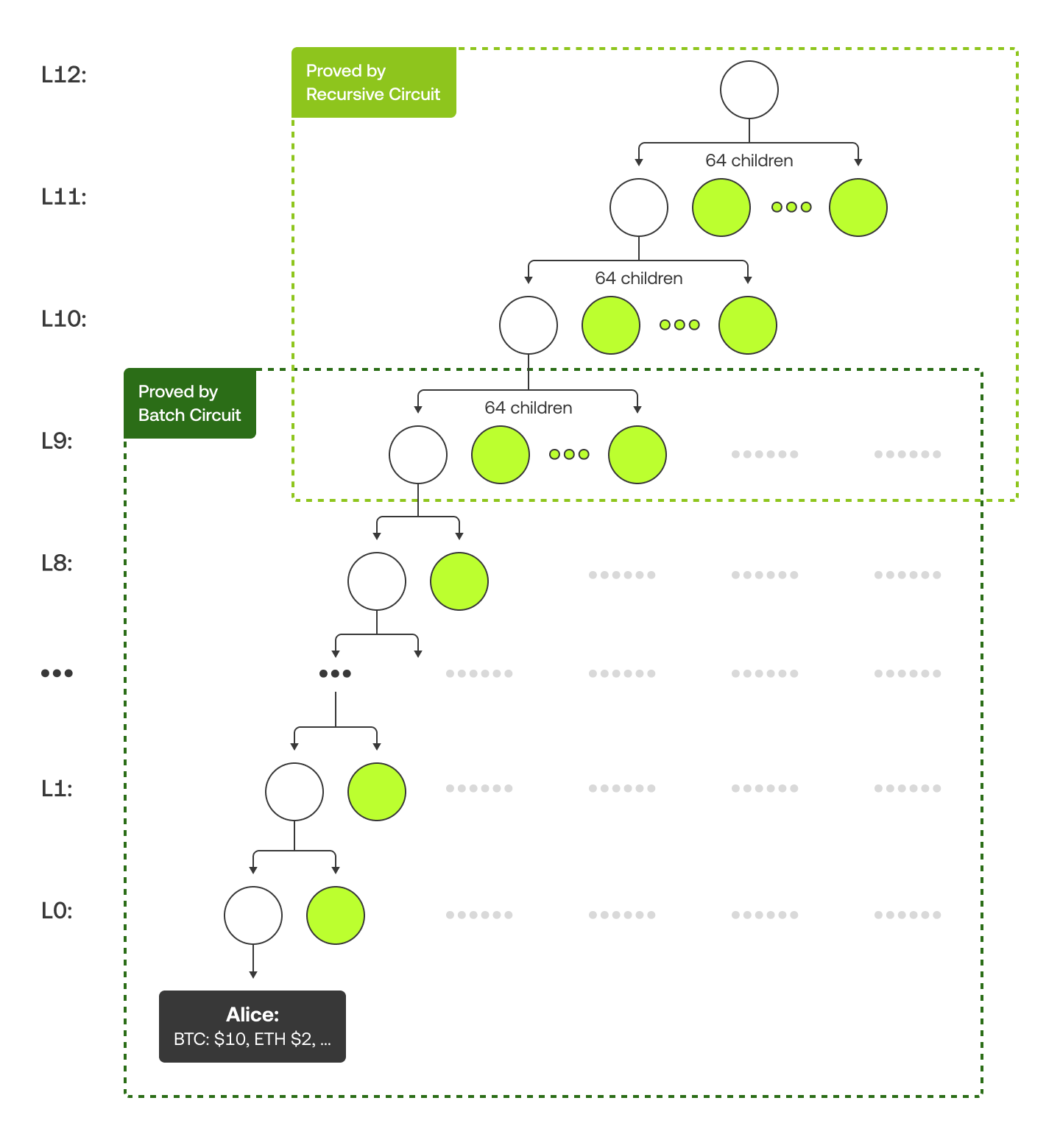
Notre arbre de Merkle est structuré un peu différemment. Dans les 10 niveaux les plus bas, chaque nœud parent a 2 enfants, tandis qu’aux niveaux supérieurs, chaque parent a 64 enfants. Cela est dû au fait que les circuits de lots gèrent la partie inférieure, et les circuits récursifs gèrent la partie supérieure. Le diagramme ci-dessous utilise un exemple avec « Alice » pour montrer l’arbre de Merkle et sa preuve de Merkle (colorée en vert).

Pour plus de détails techniques, par exemple pour savoir comment nous ajustons les numéros de compte pour s’adapter à la taille du lot ou comment nous choisissons le bon algorithme de hachage, consultez cette page.

Avancées de zk-PoR Version 2

Notre zk-PoR Version 2 affiche plusieurs avancées par rapport à la version précédente :

• Efficacité accrue : Il est maintenant 50 fois plus rapide que la version précédente. Le processus prend 3 heures sur une seule machine à 10 cœurs, contre 36 heures sur 9 machines à 64 cœurs pour la version précédente. Cette accélération est due à l’utilisation du framework Plonky2, qui compile des circuits codés en Rust en un langage machine efficace, au lieu d’utiliser des scripts Python plus lents. Nous avons également amélioré Plonky2 pour effectuer des calculs sur des GPU, réduisant le temps nécessaire de 30 % supplémentaires.

• Meilleure auditabilité : Avec la version 2, nous utilisons un framework de haut niveau qui gère pour nous des détails cryptographiques complexes. Cela rend notre code plus clair, plus lisible et moins sujet aux erreurs.

• Preuve concise : La taille de la preuve V2 (~500 Ko) représente à peine 0,05 % de la V1 (~1,2 GO). Grâce à la méthode récursive, les preuves peuvent être agrégées et condensées de manière répétée en une seule preuve.

Comment puis-je vérifier la preuve de réserves (PoR) par moi-même ?

Voici comment vérifier si le solde de vos actifs est inclus en tant que feuille Merkle zk-STARK :

1. Connectez-vous à votre compte OKX, rendez-vous dans Actifs et sélectionnez Rapports PoR

2. Sélectionnez Détails pour voir vos données d’audit

   

3. Obtenez les données dont vous avez besoin pour une vérification manuelle en sélectionnant Copier les données

   

4. Après avoir sélectionné Copier les données, ouvrez l’éditeur de texte (parexemple le bloc-notes), puis collez et enregistrez la chaîne JSON en tant que fichier. Le fichier doit se terminer par le nom « _inclusion_proof.json. » La chaîne JSON contient votre solde de compte et un instantané du chemin de Merkle, puis enregistre le fichier dans un nouveau dossier

5. Ouvrez un éditeur de texte (parexemple, le bloc-notes), puis collez et enregistrez la chaîne JSON en tant que fichier. Le nom du fichier doit se terminer par « _inclusion_proof.json. » Enregistrez le fichier dans un nouveau dossier.

   • La chaîne JSON contient le solde de votre compte et un instantané du chemin de Merkle.

   • Le texte JSON est le suivant :

     {"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}, ...... "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}

6. Téléchargez l’outil de vérification open-source OKX : zk-STARKValidator

7. Enregistrez l’outil de vérification open-source OKX, zk-STARKValidator, et placez le fichier de chaîne JSON avec dans le nouveau dossier créé à l’étape 5. Dans notre cas, nous avons placé l’outil et le fichier de données dans le dossier Téléchargements, nommé « proof-of-reserves », comme indiqué ci-dessous :

   

8. Ouvrez zk-STARKValidator ; celui-ci exécutera automatiquement le fichier JSON que vous avez enregistré dans le dossier

9. Vérifiez le résultat :

   • Si la vérification réussit, le résultat Inclusion constraint validation passed (La validation de la contrainte d’inclusion a réussi) sera affiché :

     

   • Si la vérification échoue, le résultat Inclusion constraint validation failed (La validation de la contrainte d’inclusion a échoué) sera affiché :

     

Comment vérifier le solde total zk-STARK et la contrainte non négative ?

Voici comment vérifier que les actifs que nous prétendons détenir sont réels et qu’aucun utilisateur n’a de fonds propres négatifs :

1. Rendez-vous sur notre page Preuve de réserve et sélectionnez Rapport du passif

2. Téléchargez le fichier zk-STARK et enregistrez-le dans un nouveau dossier

   

3. Dézippez le fichier pour extraire un fichier « sum_proof_data.json »

   

4. Téléchargez l’outil de vérification open-source OKX : zk-STARKValidator

5. Enregistrez l’outil de vérification open-source OKX, zk-STARKValidator, et le fichier « sum_proof_data.json » ensemble dans le nouveau dossier créé à l’étape 2. Dans notre cas, nous avons placé l’outil et le fichier de données dans le dossier Téléchargements, nommé « proof-of-reserves », comme indiqué ci-dessous :

   

6. Ouvrez zk-STARKValidator ; celui-ci exécutera automatiquement le fichier sum proof data que vous avez enregistré dans le dossier

7. Vérifiez le résultat

   • Si la vérification réussit, le résultat Total sum and non-negative constraint validation passed (La somme totale et la validation de la contrainte non négative ont réussi) sera affiché :

     

   • Si la vérification échoue, le résultat Total sum and non-negative constraint validation failed (La somme totale et la validation de la contrainte non négative ont échoué) sera affiché :

     

Pour explorer plus de détails techniques, notre système de preuve de réserves est open-source et disponible pour examen et utilisation sur github.