آليات الإثبات دون الكشف عن الهوية: ما هي تقنية إثبات المعرفة الآمن والشفاف والمُتكيِّف (ZK-STARK) وما آلية عملها؟ (الإصدار الثاني من zk-Stark)

ما المقصود بإثبات الاحتياطيات وآلية الإثبات دون الكشف عن الهوية؟

إثبات الاحتياطيات (PoR)

هي عملية تستخدمها منصات تداول العملات الرقمية لتُظهر امتلاكها لأصول كافية تُغطّي جميع أرصدة العملاء. تُسهم هذه العملية في بناء الثقة من خلال إثبات أنَّ المنصة لا تُخفي أي التزامات مالية. ولعلّ الطريقة الأبسط لإثبات ذلك تتمثّل في نشر المبالغ التي تمتلكها المنصة من الأصول إلى جانب قائمة بأرصدة المستخدمين، بحيث يتمكن الجميع من التحقّق ممّا يلي:

• أنّ إجمالي حيازات المستخدمين من الأصول التي تدّعي منصة OKX أنّها تحتفظ بها هو بالفعل مجموع أرصدة جميع المستخدمين.

• أنّ إجمالي رصيد كل مستخدم يزيد عن الصفر (ليس سالبًا)، وأنّ أصولهم مُسجّلة وموّثقة لدى المنصة لضمان تغطية أي التزامات مالية تخصّهم وضمان امتلاك كل منهم لصافي قيمة حساب موجبة.

• القيمة الإجمالية التي تدّعي المنصة أنها تُغطّي جميع المستخدمين، إذ يجب أن يتمكّن كل مستخدم من التحقّق من كون القيمة الإجمالية التي تحتفظ بها المنصة تشمل صافي قيمة حسابه بالفعل.

إلّا أنّ الكشف عن هذه الأرصدة قد يعرّض خصوصية المستخدمين للخطر. ولحل هذه المشكلة، نستخدم طريقة تُعرف باسم آلية الإثبات دون الكشف عن الهوية (ZKP) لحماية خصوصية المستخدمين

آلية الإثبات دون الكشف عن الهوية (ZKP)

هي تقنية أمان تتيح لمنصة تداول العملات الرقمية إثبات صحة بيان معيّن دون الإفصاح عن أي معلومات إضافية.

وبالنسبة لنا، فإنّنا نرغب في إثبات امتلاكنا لأموال كافية دون الكشف عن تفاصيل المستخدمين. تندرج معظم آليات الإثبات دون الكشف عن الهوية ضمن فئتين:

• تقنية الإثبات دون الكشف عن الهوية الموجزة غير التفاعلية (ZK-SNARK)

• تقنية إثبات المعرفة الآمن والشفاف والمُتكيِّف (ZK-STARK)

نستخدم تقنية ZK-STARK نظرًا لأنها أكثر أمانًا وتتطلّب أقل افتراضات أمان (تُحقّق الأمان على نحوٍ مستقل تقريبًا، دون الحاجة إلى الاعتماد على العديد من الافتراضات أو العوامل الخارجية لتأمين النظام). سنشرح في هذا المقال كيفية استخدامنا لتقنية ZK-STARK لحماية خصوصية المستخدمين في إطار إثبات قدرتنا على الوفاء بالالتزامات المالية.وقبل الخوض في ذلك، لعلّه من المفيد التعرّف على بعض المصطلحات الأساسية المُتعلّقة بآلية الإثبات دون الكشف عن الهوية، من قبيل نماذج الدارات (Circuit - نماذج رياضية تُستخدم لتمثيل العمليات الحسابية التي يجب أن يُثبتها النظام، وتُعدّ بالنتيجة تقنية تشفير تُحوّل المسائل المُعقدّة إلى سلسلة من الخطوات الحسابية المُبسّطة التي يمكن التحقّق منها دون الكشف عن تفاصيل البيانات الأصلية)، وشجرة التجزئة الثنائية (Merkle Tree - بنية معطيات تُستخدم لتشفير كافة بيانات البلوكتشين، ممّا يضمن عدم التلاعب بها والتحقّق منها على نحو فعال)، والالتزامات (Commitments - بروتوكولات تشفير تسمح لطرف ما بإخفاء قيمة معينة في صندوق افتراضي بحيث يمكن للطرف الآخر أن يعرف بوجود هذه القيمة دون الاطّلاع عليها إلى حين فتح هذا الصندوق من قبل المُرسل، وبمجرّد الالتزام بالقيمة لا يمكن للمرسل تغييرها، وبالتالي هي آلية للتحقّق دون إفصاح).

بالنسبة للمبتدئين، تتوفّر العديد من الموارد لمساعدتك كنقطة انطلاق. أمّا للمستخدمين المُتقدمّين، فيمكنكم الرجوع إلى هذا المساق التعليمي المُكثفّ مفتوح المصدر عبر الإنترنت (MOOC) أو هذه الدراسة الأكاديمية.

كيف تعمل تقنية ZK-STARK؟

ننشئ شجرة تجزئة ثنائية باستخدام رمز التجزئة الخاص بكل حساب مستخدم كأوراق لشجرة التجزئة الثنائية (leaves - العُقد الطرفية في شجرة التجزئة الثنائية، وهي أوّل طبقة من العُقد في أسفل الشجرة والتي تُستخدم كبداية لعملية البناء الهرمي للشجرة، فبدمج كل زوج من الأوراق في كل مستوى من الشجرة، يتم احتساب الطبقة التالية تدريجيًا، وصولًا إلى جذر الشجرة الذي يتضمّن مُجمل بياناتها). يعرض كل حساب الأرصدة مُقدرّة بالدولار الأمريكي لمختلف العملات الرمزيّة(من قبيل، BTC وETH). وللتعامل مع هذه الأرصدة حسابيًا، نفصلها إلى قيم موجبة للحسابات وديون لكل عملة رمزيّة (بمعنى تحويل الأرصدة السالبة إلى ديون نتعامل معها كقيم موجبة). بحيث نتعامل فقط مع الأرقام الموجبة ممّا يسهل عمليات الحساب ويقلل من احتمالات الأخطاء.

فعلى سبيل المثال:

• إذا كان رصيد المستخدم بعملة BTC يبلغ المقدار A، فتكون قيمة حسابه من BTC هي A، والديون تبلغ 0.

• أمّا إذا كان رصيد المستخدم بعملة ETH مثلًا يبلغ -B، فتكون قيمة حسابه الموافقة 0، في حين تكون قيمة الديون هي B، وبذلك نتخلّص من القيم السالبة.

لنبني بعد ذلك شجرة التجزئة الثنائية باستخدام هذه قيم المُستنتجة من حسابات المستخدمين كأوراق للشجرة. وصولًا إلى جذر الشجرة، والذي يتضمّن قيمة واحدة تُمثّل جميع أرصدة المستخدمين (مُجمل بيانات الشجرة). وبذلك يمكن لكل مستخدم إثبات أن حسابه جزء من هذه الشجرة باستخدام مسار شجرة التجزئة (Merkle Path) الذي يوضّح كيفية اتصال حسابه بجذر الشجرة.

كما ننشر إجمالي قيم الحسابات والديون مجمّعةً لجميع العملات الرمزيّة ولجميع المستخدمين. ومن ثم نُنشئ إثباتًا دون الكشف عن الهوية لإظهار أمرين:

• إثبات المجموع: أي أنّ قيم الحسابات والديون في شجرة التجزئة الثنائية قد جُمعت على نحوٍ صحيح.

• إثبات عدم وجود قيم سالبة: بمعنى أنّ إجمالي قيمة الحساب لكل مستخدم أعلى من إجمالي ديونه.

ولكن، عند محاولة التحقّق من شجرة التجزئة الثنائية لعدد كبير من الحسابات، قد يصبح من الصعب معالجتها دُفعةً واحدة. وللتغلّب على هذه العقبة، نُقسّم إجمالي عدد الحسابات ضمن مجموعاتٍ أصغر تسمى الدُفعات. لتتم معالجة كل دفعة على نحوٍ منفصل باستخدام نماذج دارات معالجة الدُفعات (batch circuits)، والتي تتحقّق من الجزء السفلي لشجرة التجزئة الثنائية المُتضمّن لبيانات حسابات المستخدمين المُشفّرة على نحوٍ فرديّ.

فآلية تجميع الحسابات في هيئة دُفعات لا تجعل من إدارتها أمرًا ممكنًا فحسب، بل تمكنّنا من إجراء عمليات التحقّق على نحوٍ متزامن (المعالجة المتوازية). وبمجرّد الحصول على النتائج من كل دُفعة، نستخدم طبقة إضافية من نماذج الدارات تسمّى نماذج دارات المعالجة التكرارية (recursive circuits) لتجميع هذه الدُفعات معًا والتحقّق منها، إلى حين إثبات صحّة شجرة التجزئة بالكامل.

ما هو نموذج دارات معالجة الدُفعات؟

يأخذ نموذج دارات معالجة الدُفعات 1024 حسابًا (acc₀، acc₁وهكذا حتىacc₁₀₂₃) كمدخلات ليُنتج ثلاث مخرجات رئيسية، وهي: رمز التجزئة للدُفعة (h_batch)، وإجمالي قيم حسابات الدُفعة (e_batch)، وقيمة إجمالي الديون للدُفعة (d_batch). ويتحقّق النموذج ممّا يلي:

• أنّ إجمالي قيمة كل حساب بعملة أساس USD أعلى من إجمالي الديون.

• أنّ إجمالي قيم حسابات الدُفعة e_batch يُمثّل مجموع إجمالي قيمة كل حساب بعملة أساس USD من حسابات الدُفعة.

• أنّ قيمة إجمالي الديون للدُفعة d_batch يُمثّل مجموع قيم الديون بعملة أساس USD لكل من حسابات الدُفعة.

• أنّ رمز التجزئة للدُفعة h_batch يُمثّل جذر شجرة تجزئة ثنائية ناتجة باستخدام رموز التجزئة الخاصّة بهذه الحسابات (بمعنى أنّ رمز التجزئة للدُفعة يتضمّن معلومات كافّة رموز التجزئة لكل حسابات الدُفعة).

• عدم وجود فائض بتجاوز السعة (overflow - حالة تحدث عندما تتجاوز نتيجة عملية حسابية ما السعة القصوى التي يمكن للنظام أو المتغير تخزينها) في المجموع عند حساب القيم لكل من e_batch وd_batch

ما هو نموذج دارات المعالجة التكرارية؟

يأخذ نموذج دارات المعالجة التكرارية 64 إثباتًا مختلفًا (π₀،وهكذا حتىπ₆₃)، ورموز تجزئة (h₀،وهكذا حتىh₆₃)، وإجمالي قيم الحسابات (e₀،وهكذا حتىe₆₃₎، والديون (d₀،وهكذا حتىd₆₃) من نماذج الدارات في الطبقة الأدنى كمُدخلات. إذ يُجمّع النموذج هذه المدخلات لإنتاج ثلاثة مخرجات، وهي: رمز تجزئة جديد (h_recursive)، وإجمالي قيمة الحسابات (e_recursive)، وإجمالي الديون (d_recursive). ويتحقّق النموذج ممّا يلي:

• صحّة كل من الإثباتات البالغ عددها 64.

• صحّة كل إثبات π₀،وهكذا حتىπ₆₃ من نواتج نموذج دارات الطبقة الأدنى (نموذج دارات معالجة الدُفعات).

• أنّ إجمالي قيمة الحسابات e_recursive يمثّل مجموع e₀،وهكذا حتىe₆₃

• أنّ إجمالي الديون d_recursive يمثّل مجموع d₀،وهكذا حتىd₆₃

• أنّ رمز التجزئة h_recursive يُمثّل بالفعل رمز تجزئة ناتج عن تجميع h₀،وهكذا حتىh₆₃،أي

  • h_recursive = Hash (h₀ || h₁ || .وهكذا حتى || h₆₃₎ (علمًا أنّ || تعني concatenation بمعنى التجميع).

• عدم وجود فائض بتجاوز السعة في المجموع عند احتساب نواتج عمليات الجمع لكل من e_recursive وd_recursive

ما هي العلاقة بين نماذج دارات معالجة الدُفعات ونماذج دارات المعالجة التكرارية؟

يوضّح الرسم التخطيطي أدناه كيفية اتصال نماذج دارات معالجة الدُفعات بنماذج دارات المعالجة التكرارية وآلية نقل البيانات بين بعضها البعض. يُرجى ملاحظة أنّه في الرسم التخطيطي نكُرّر نماذج الدارات لأغراض التوضيح، ولكن في التطبيق الفعلي نستخدم نموذج دارات واحد لكل طبقة.

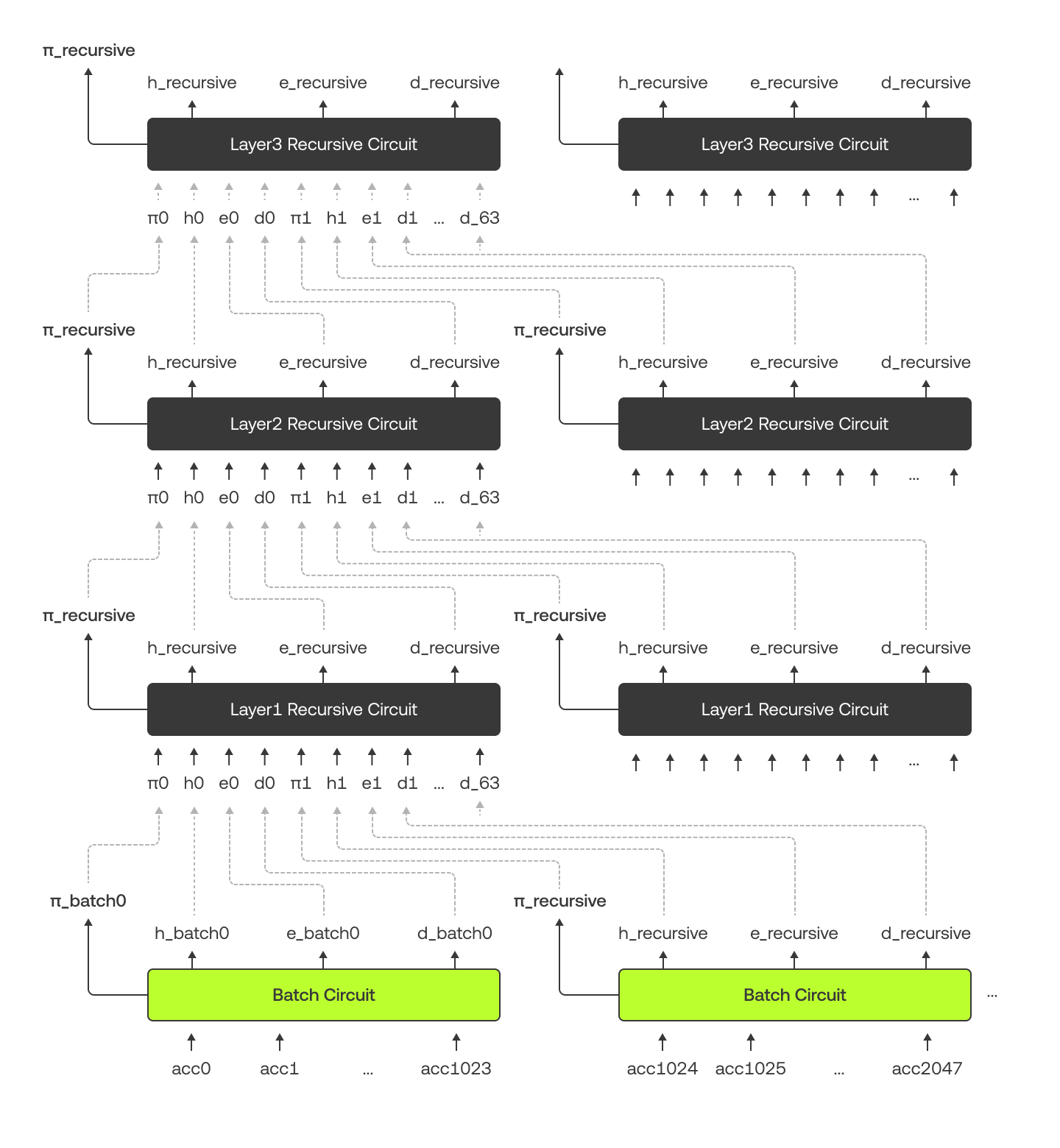
تختلف بنية شجرة التجزئة الثنائية لدينا بعض الشيء عن بنية الشجرة التقليدية (والتي يكون فيها لكل عقدة رئيسية -أب- عقدتين فرعيتين -أبناء- فقط). ففي المستويات السفلية العشرة، يتفرّع عن كل عقدة رئيسية عقدتين فرعيتين، بينما يتفرّع عن كل عقدة رئيسية في المستويات العليا 64 عقدة فرعية. يُعزى ذلك إلى أنّ نماذج دارات معالجة الدُفعات تتعامل مع الجزء السفلي من الشجرة، في حين تتولّى نماذج دارات المعالجة التكرارية إدارة الجزء العلوي. ويوضّح الرسم التخطيطي أدناه مثالًا باستخدام حساب مُستخدمة تُدعى «Alice» لعرض شجرة التجزئة الثنائية والإثبات الخاص بها وفق مسار حسابها في الشجرة (الموضّح باللون الأخضر).

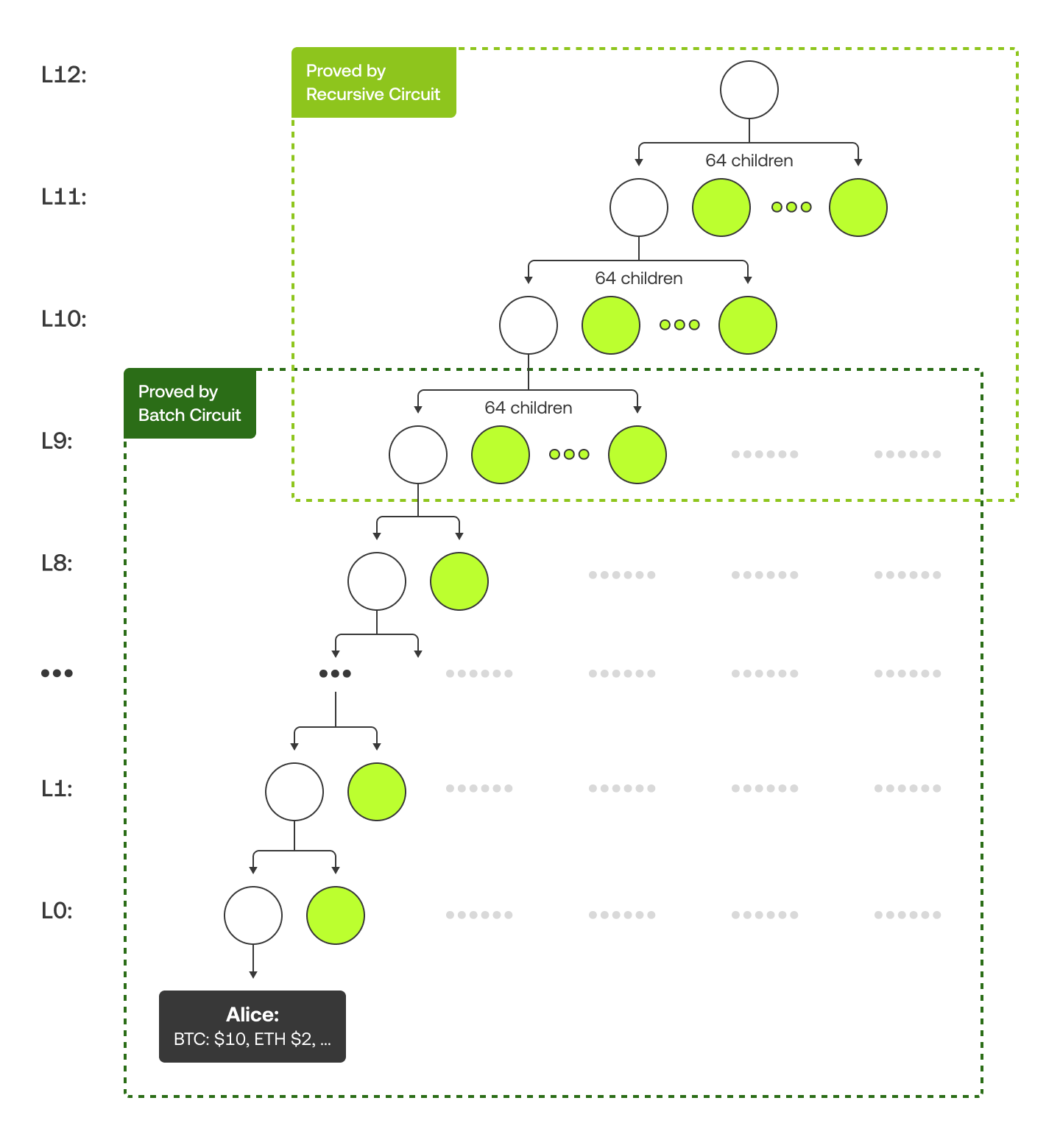
لمزيدٍ من التفاصيل التقنية من قبيل كيفية ضبط أرقام الحسابات لتلائم حجم الدُفعة أو كيفية اختيار خوارزمية التجزئة المناسبة، اطّلع على هذه الصفحة.

التطوّرات في الإصدار الثاني من إثبات الاحتياطيات دون الكشف عن الهوية (zk-PoR Version 2)

حقّق الإصدار الثاني من إثبات الاحتياطيات دون الكشف عن الهوية لدينا تحسيناتٍ كبيرة مقارنةً بالإصدار السابق:

• كفاءة أعلى: الإصدار الثاني أسرع بحدود 50 مرة مقارنةً بالإصدار السابق. إذ يتطلب 3 ساعات باستخدام جهاز واحد بمعالج يتضمّن 10 نوى، مقارنةً مع 36 ساعة في الإصدار السابق باستخدام تسعة أجهزة كل منها بمعالج يتضمّن 64 نواة لكل منها. يعود هذا التسريع إلى استخدام إطار Plonky2 (هو إطار عمل يجمع بين مزايا SNARKs وSTARKs يتميز بسرعته مقارنةً بالبدائل الحالية، إذ يوفّر إثباتات سريعة وفعالة، ويدعم الآلية العودية برمجيًا -استدعاء نفس الدالّة البرمجية لنفسها على نحوٍ مُتكرّر- بكفاءة عالية)، والذي يحوّل نماذج الدارات المكتوبة بلغة Rust إلى لغة الآلة بكفاءة، بدلًا من استخدام نصوص برمجية مكتوبة بلغة Python التي تستغرق وقتًا أكبر في المعالجة (إلى حين ترجمتها وتجميعها وربطها لتحويلها إلى لغة الآلة). كما تمّت ترقية إطار Plonky2 لتشغيل بعض العمليات على وحدات معالجة الرسومات (GPU) بالتوازي مع المعالج، ممّا يقلل من الوقت اللازم بنسبة 30% إضافية.

• تحسين آلية التدقيق: نستخدم في الإصدار الثاني إطار عمل عالي المستوى يتولّى تفاصيل التشفير المُعقدّة نيابةً عنّا. ممّا يجعل الأكواد البرمجية أوضح، وأكثر قابلية للقراءة (معيار يُعبّر عن وضوح الكود البرمجي من حيث إمكانية فهم مبرمج آخر لتفاصيل هذا الكود - الأمر يتعلّق بنظافة الكود من حيث التنظيم وإضافة التعليقات وغيرها)، وأقل عرضة للأخطاء.

• إثبات مختصر من حيث الحجم إذ يبلغ حجم إثبات الإصدار الثاني (حوالي 500KB) ما يُمثّل 0.05% فقط من حجم الإصدار الأول البالغ (حوالي 1.2 GB). فبفضل الآلية العودية، يمكن تجميع الإثباتات ودمجها على نحوٍ مُتكرّر في إثبات واحد مختصر.

كيف يمكنني إجراء التحقّق الذاتي من إثبات الاحتياطيات (PoR)؟

إليك كيفية التحقّق مّما إذا كان رصيد أصولك مشمولًا كورقة من أوراق شجرة التجزئة الثنائية وفق تقنية ZK-STARK:

1. سجّل الدخول إلى حسابك لدى OKX، ثم انتقل إلى الأصول واختر تقارير إثبات الاحتياطيات

2. اضغط على التفاصيل للاطّلاع على بيانات التدقيق الخاصّة بك

   

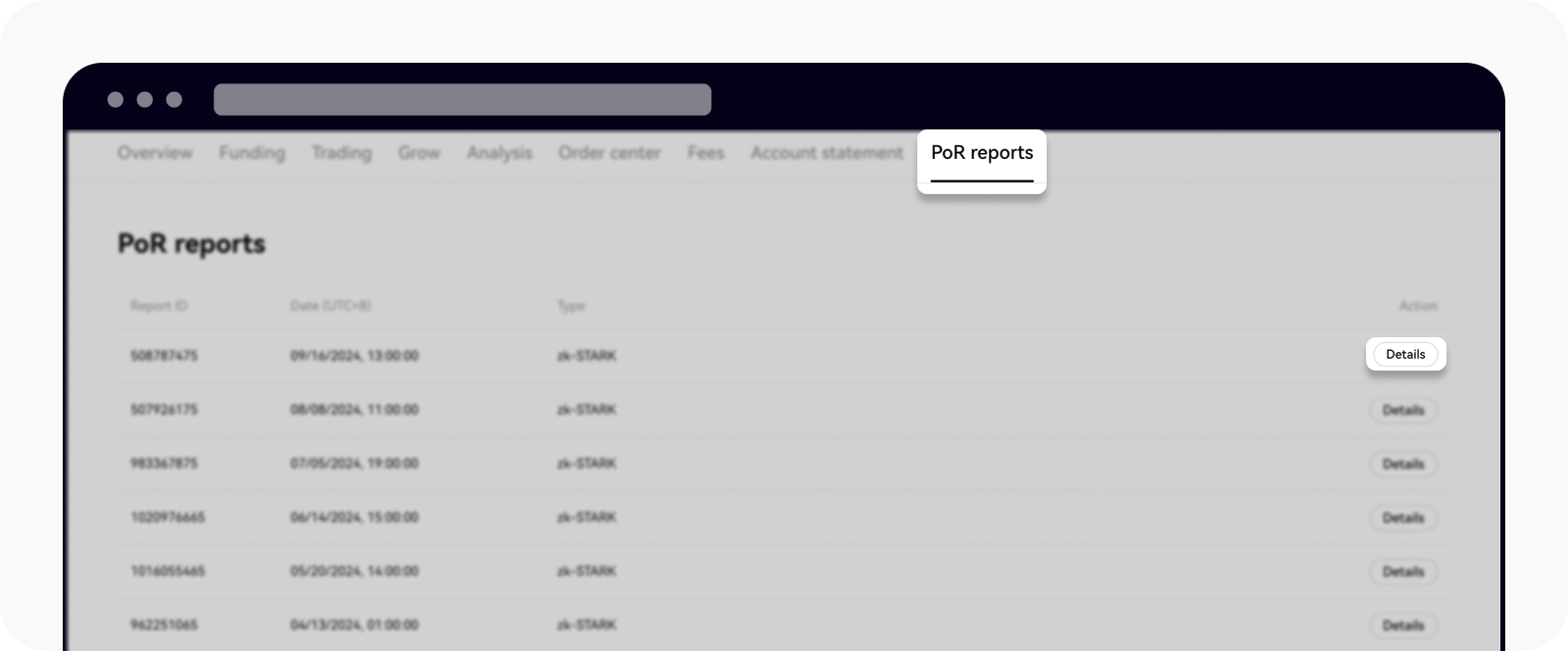
3. احصل على البيانات اللازمة للتحقّق اليدوي بالنقر على نسخ البيانات

   

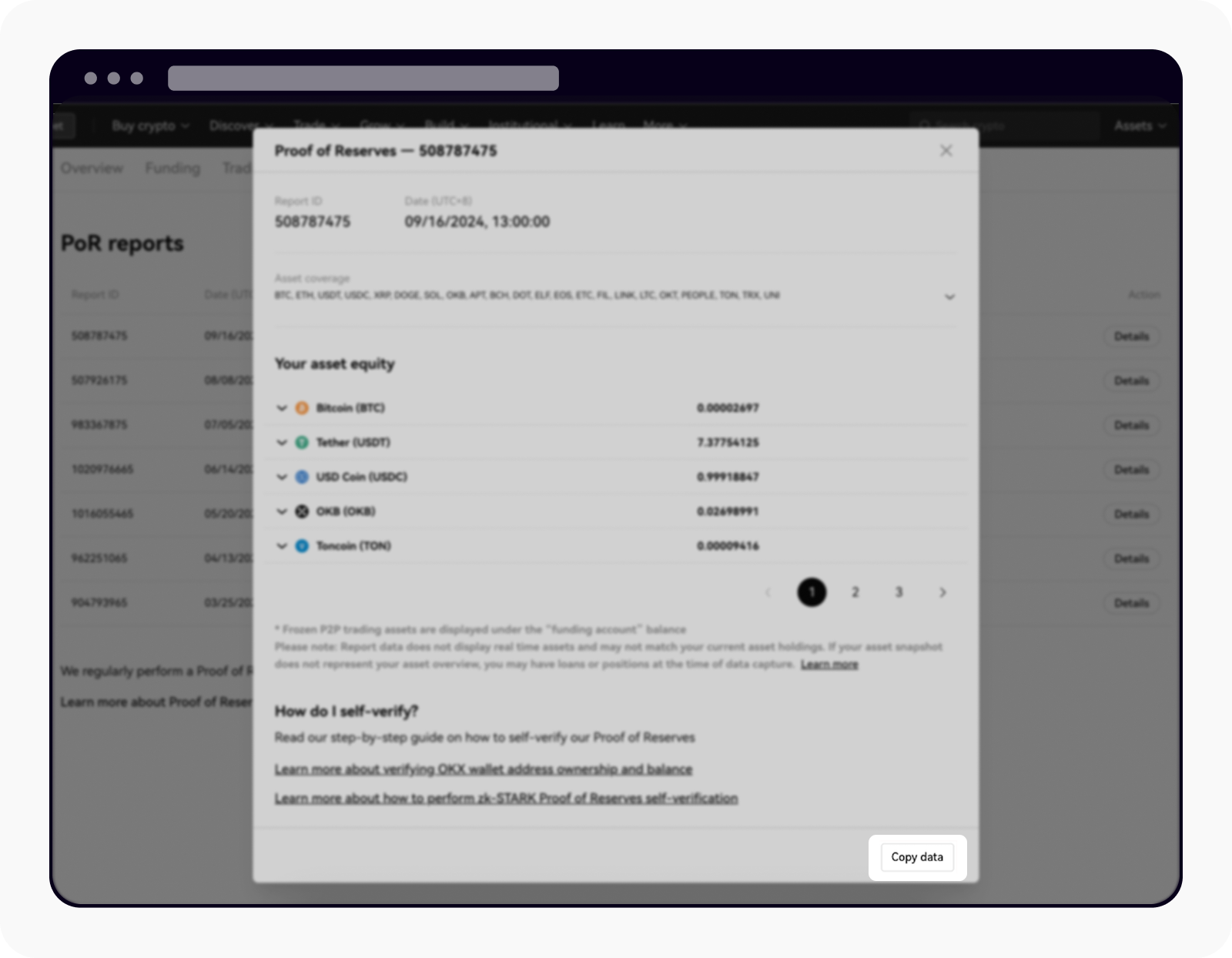
4. بعد الضغط على نسخ البيانات، افتح أي مُحرّر نصوص(من قبيل برنامج المُفكّرة Notebook)، ثم الصق النص المُنسّق بصيغة JSON () واحفظ الملف. يجب أن ينتهي اسم الملف باللاحقة «_inclusion_proof.json.» إذ يتضمّن النص المُنسّق بصيغة JSON كل من رصيد حسابك والمسار ضمن شجرة التجزئة الثنائية، ثم احفظ الملف في مجلد جديد.

5. افتح أي مُحرّر نصوص(من قبيل، برنامج المُفكّرة Notebook)، ثم الصق النص المُنسّق بصيغة JSON واحفظ الملف. يجب أن ينتهي اسم الملف باللاحقة «_inclusion_proof.json.» ثم احفظ الملف في مجلد جديد.

   • يتضمّن النص المُنسّق بصيغة JSON كل من رصيد حسابك والمسار ضمن شجرة التجزئة الثنائية.

   • النص المُنسّق بصيغة JSON مُبيّن أدناه:

     {"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}, ...... "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}

6. قم بتنزيل أداة التحقّق مفتوحة المصدر من OKX، والمسمّاة: zk-STARKValidator (أي أداة التدقيق وفق تقنية إثبات المعرفة الآمن والشفاف والمُتكيِّف)

7. احفظ أداة التحقّق مفتوحة المصدر من OKX المُسمّاة zk-STARKValidator، والملف النصي وفق تنسيق JSON في المجلد الجديد الذي أنشأته في الخطوة الخامسة (5). في مثالنا، وضعنا الأداة وملف البيانات (ملف JSON) في مجلد التنزيلات، وأسميناه «proof-of-reserves»، كما هو موضّح أدناه:

   

8. افتح أداة zk-STARKValidator، إذ ستعمل تلقائيًا على تشغيل ملف JSON الذي قمت بحفظه في نفس المجلد

9. تحقّق من النتيجة:

   • إذا نجح التحقّق، فستظهر النتيجة تم اجتياز التحقّق من صحّة قيد إدراج الأصول في الإثبات:

     

   • إذا فشل التحقّق، فستظهر النتيجة فشل التحقّق من صحّة قيد إدراج الأصول في الإثبات:

     

كيف يمكنني التحقّق من إجمالي رصيدي وفق تقنية ZK-STARK والتحقّق من عدم وجود قيود سالبة؟

إليك كيفية التحقّق من صحة الأصول التي ندّعي امتلاكها، والتأكّد من عدم امتلاك أي مستخدم لصافي قيمة حساب سالب:

1. انتقل إلى صفحة إثبات الاحتياطيات واختر تقرير الالتزامات المالية

2. حمّل الملف الخاص بتقنية ZK-STARK واحفظه في مجلد جديد

   

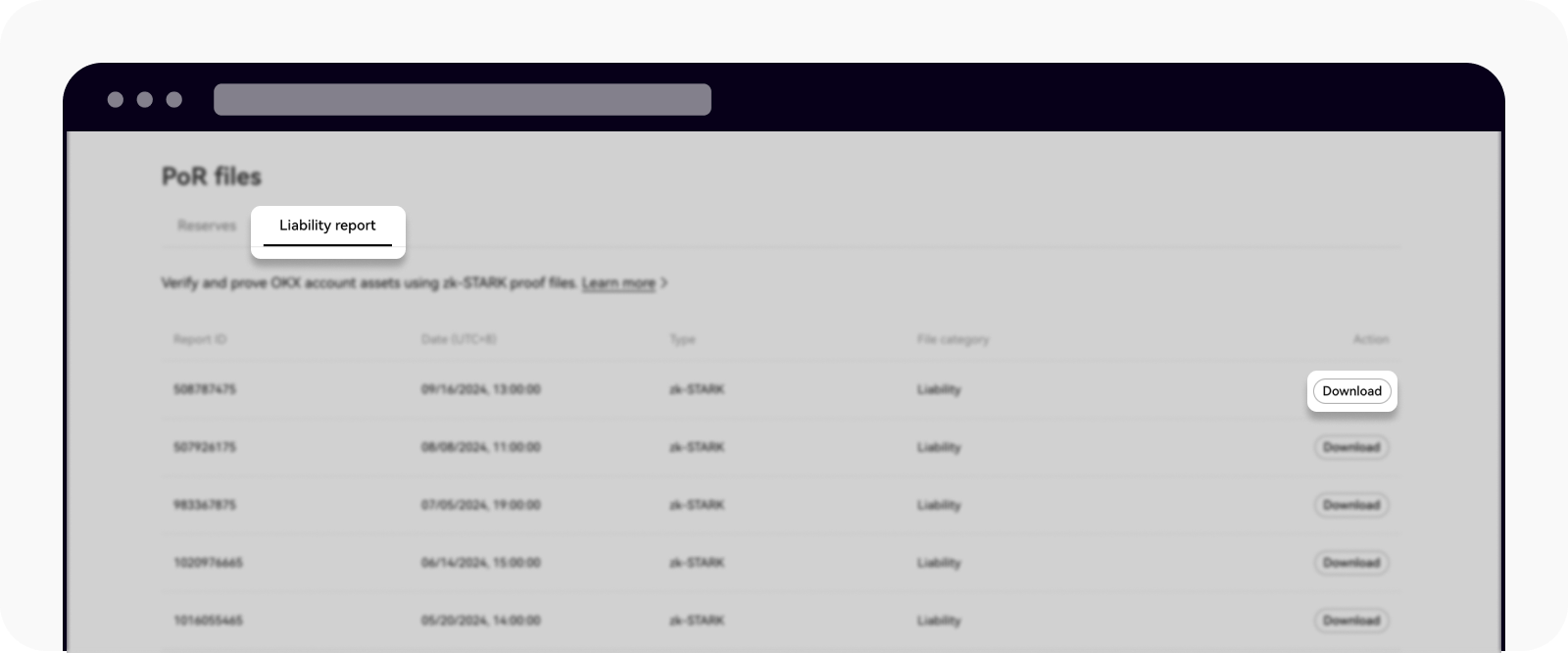
3. قم بفك ضغط الملف لاستخراج ملف «sum_proof_data.json»

   

4. قم بتنزيل أداة التحقّق مفتوحة المصدر من OKX، والمسمّاة: zk-STARKValidator (أي أداة التدقيق وفق تقنية إثبات المعرفة الآمن والشفاف والمُتكيِّف)

5. احفظ أداة التحقّق مفتوحة المصدر من OKX، والمسمّاة: zk-STARKValidator والملف «sum_proof_data.json» في المجلد الجديد الذي تم إنشاؤه في الخطوة الثانية (2). في مثالنا، وضعنا الأداة وملف البيانات (ملف JSON) في مجلد التنزيلات، وأسميناه «proof-of-reserves»، كما هو موضّح أدناه:

   

6. افتح أداة zk-STARKValidator؛ إذ ستعمل تلقائيًا على تشغيل الملف sum proof data (بيانات إثبات المجموع) الذي حفظته في نفس المجلد.

7. تحقّق من النتيجة

   • إذا نجح التحقّق، فستظهر النتيجة تم اجتياز التحقّق من المجموع وعدم انتهاك قيد القيم السالبة:

     

   • إذا فشل التحقّق، فستظهر النتيجة فشل التحقّق من المجموع وعدم انتهاك قيد القيم السالبة:

     

للاطلاع على المزيد من التفاصيل التقنية، فإنّ نظام إثبات الاحتياطيات PoR الخاص بنا متاح ومفتوح المصدر ومتوفّر للمراجعة والاستخدام على نظام التحكّم بالإصدارات GitHub.